符号有向图(Signed Directed Graph,SDG)是一种基于模型方法的故障识别与诊断技术,是一种定性表示因果关系的图论方法。符号有向图(SDG)是定性研究化工过程中变量间关系的有力工具,利用SDG的正向反向推理机制可以快速发掘出系统中变量之间影响的因果关系,不仅可以用于在线的故障诊断,还可以用于离线的危险和可操作性(HAZOP)分析。
在线的SDG推理系统
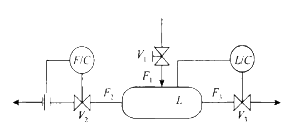
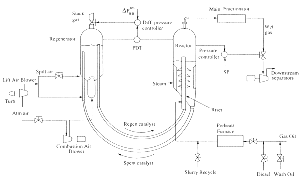
水箱体系如下图所示。
对于的SDG模型及推理运行的结果如下:
import sdg
digraph_content=”’digraph buffer_tank {
node [style=filled];
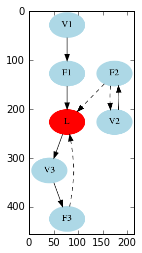
V1->F1[style=solid];
F1->L[style=solid];
L->V3[style=solid];
V2->F2[style=solid];
V3->F3[style=solid];
F2->L[style=dashed];
F2->V2[style=dashed];
F3->L[style=dashed];}
”’
set_nodes_init_state={‘V1′:1}
steps=2
sdg.sdg_run_forward(steps,digraph_content,set_nodes_init_state)
img = pylab.imread(‘digraph.png’)
pylab.imshow(img)
pylab.show()
推理结果
Nodes list: ['F1', 'F2', 'F3', 'L', 'V1', 'V2', 'V3'] Adjacency matrix: [[ 0 0 0 1 0 0 0] [ 0 0 0 -1 0 -1 0] [ 0 0 0 -1 0 0 0] [ 0 0 0 0 0 0 1] [ 1 0 0 0 0 0 0] [ 0 1 0 0 0 0 0] [ 0 0 1 0 0 0 0]]
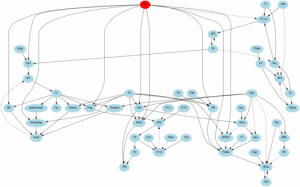
import sdg
digraph_content=”’digraph CSTR{
node [style=filled];
size=”8,8″;
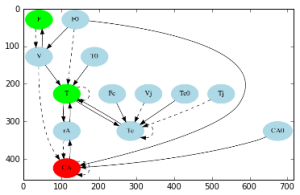
F->V[style=dashed];
V->F[style=solid];
V->CA[style=dashed];
V->T[style=solid];
CA->CA[style=dashed];
CA->rA[style=solid];
CA0->CA[style=solid];
F0->V[style=solid];
F0->CA[style=solid];
F0->T[style=dashed];
T->T[style=dashed];
T->rA[style=solid];
T->Tc[style=solid];
rA->CA[style=dashed];
rA->T[style=solid];
T0->T[style=solid];
Fc->Tc[style=solid];
Tc->T[style=solid];
Tc->Tc[style=dashed];
Vj->Tc[style=dashed];
Tc0->Tc[style=solid];
Tj->Tc[style=dashed];
}
”’
init_state={‘F’:1}
steps=2
sdg.sdg_run_forward(steps,digraph_content,init_state)
img = pylab.imread(‘digraph.png’)
pylab.imshow(img)
pylab.show()
推理结果
Nodes list: ['CA', 'CA0', 'F', 'F0', 'Fc',..., 'Tj', 'V', 'Vj', 'rA'] Adjacency matrix: [[-1 0 0 0 0 0 0 0 0 0 0 0 1] [ 1 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 -1 0 0] [ 1 0 0 0 0 -1 0 0 0 0 1 0 0] [ 0 0 0 0 0 0 0 1 0 0 0 0 0] [ 0 0 0 0 0 -1 0 1 0 0 0 0 1] [ 0 0 0 0 0 1 0 0 0 0 0 0 0] [ 0 0 0 0 0 1 0 -1 0 0 0 0 0] [ 0 0 0 0 0 0 0 1 0 0 0 0 0] [ 0 0 0 0 0 0 0 -1 0 0 0 0 0] [-1 0 1 0 0 1 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 -1 0 0 0 0 0] [-1 0 0 0 0 1 0 0 0 0 0 0 0]]
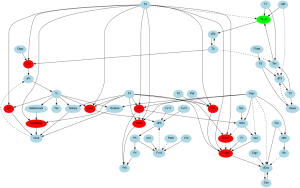
import sdg
#PCA-SDG FCCU
digraph_content=”’digraph FCCU{
node [style=filled];
size=”8,8″;
Qrgc->Qm[style=solid];
Qm->dTr[style=solid];
dTr->Tr[style=solid];
Patm->Fv12[style=dashed];
V12->Fv12[style=solid];
k12->Fv12[style=solid];
Fv12->dP5[style=dashed];
Fv11->dP5[style=dashed];
dP5->P5[style=solid];
P5->Fv12[style=solid];
P5->P4[style=solid];
Fv13->dP5[style=solid];
P4->Prb[style=solid];
Qout->dTr[style=dashed];
Qslurry->Qout[style=solid];
Qcracking->Qout[style=solid];
Qcatout->Qout[style=solid];
Qff->Qout[style=solid];
F1->Fcoke[style=solid];
F2->FB[style=solid];
FB->Fcoke[style=solid];
Psif->FB[style=solid];
WSHV->Fcoke[style=dashed];
Fcoke->dCsc[style=solid];
F3->Qcracking[style=solid];
F3->Qff[style=solid];
F3->Qm[style=solid];
F3->FB[style=solid];
F3->WSHV[style=solid];
F3->Fcoke[style=solid];
F3->rhoris[style=solid];
F3->Vris[style=solid];
F3->Fwg[style=solid];
F3->T2_ss[style=dashed];
Fwg->dP5[style=solid];
Tr->Fwg[style=solid];
Tr->Tsc[style=solid];
Tr->deltaHcrack[style=solid];
Tr->Qslurry[style=solid];
Tr->Qcatout[style=solid];
Tr->Qff[style=solid];
deltaHcrack->Qcracking[style=solid];
UAf->T2_ss[style=solid];
UAf->dT3[style=dashed];
T2_ss->dT2[style=solid];
F4->Qslurry[style=solid];
F4->Qcracking[style=solid];
F4->Fwg[style=solid];
F4->FB[style=solid];
F4->Fcoke[style=solid];
F4->WSHV[style=solid];
F4->rhoris[style=solid];
F4->Vris[style=solid];
taur->Fcoke[style=solid];
dWr->Wr[style=solid];
Wr->dCsc[style=dashed];
dCsc->Csc[style=solid];
Crgc->dCsc[style=solid];
Csc->dCsc[style=solid];
Fsc->dCsc[style=solid];
Fsc->dWr[style=dashed];
Frgc->dWr[style=solid];
Frgc->dCsc[style=dashed];
Frgc->rhoris[style=solid];
Frgc->Vris[style=solid];
Frgc->Wris[style=solid];
Frgc->Qcatout[style=solid];
Frgc->taur[style=dashed];
rhoris->Prb[style=solid];
Vris->rhoris[style=dashed];
Vris->Prb[style=solid];
Vris->Wris[style=solid];
Wris->WSHV[style=dashed];
Wris->taur[style=solid];
hris->Wris[style=solid];
dT2->T2[style=solid];
T2->dT2[style=dashed];
T2->Tlm[style=dashed];
T2->Qm[style=solid];
T1->T2_ss[style=solid];
T1->Tlm[style=solid];
Tlm->T2_ss[style=solid];
Tlm->dT3[style=dashed];
T3->Tlm[style=solid];
T3->Qloss[style=solid];
dT3->T3[style=solid];
Qloss->dT3[style=dashed];
F5->Qloss[style=solid];
F5->dT3[style=solid];
F5set->F5[style=solid];
}
”’
init_state={‘Qrgc’:1}
steps=2
sdg.sdg_run_forward(steps,digraph_content,init_state)
img = pylab.imread(‘digraph.png’)
pylab.imshow(img)
pylab.show()
推理结果
Nodes list: ['Crgc', 'Csc', 'F1', 'F2', 'F3', 'F4', 'F5',..., 'rhoris', 'taur'] Adjacency matrix: [[0 0 0 ..., 0 0 0] [0 0 0 ..., 0 0 0] [0 0 0 ..., 0 0 0] ..., [0 0 0 ..., 0 0 0] [0 0 0 ..., 0 0 0] [0 0 0 ..., 0 0 0]]